|
От энтропии черной дыры к сложности листьев растений
|
| Сложность биологических форм очаровывала человечество на протяжении многих лет. Разные виды растений имеют разную форму листьев. Вы когда-нибудь задумывались, почему это так? Почему существует такое разнообразие форм? Растения могут менять форму листьев со временем и в пространстве. Но как? Играет ли особая форма листьев значительную роль в оптимизации энергопотребления? Фактически, форма листьев во многом связана с адаптацией к окружающей среде. Как раскрытие формы связано с эволюционным процессом природы? Эти интригующие вопросы заставили нас сосредоточиться на количественных подходах к изучению сложности листьев растений. Количественная оценка формы листьев с использованием евклидовых фигур, таких как круги, треугольники и т. д., подходит лишь для некоторых видов растений. Поэтому с разной точностью разработаны различные количественные меры формы листьев. Но действительно ли форма объекта является его реальной формой? Зрительное восприятие определенной формы или геометрии физических объектов является лишь абстракцией. Если копнуть глубже в существование формы, то окажется, что закономерности и границы, которые мы видим, не идеальны. Форма и границы любого физического объекта — это всего лишь восприятие человеческого зрения. Реалистичная граница будет меняться с увеличением и может восприниматься как размытая микромасштабная граница раздела с конечной толщиной. |
|
| Как связаны геометрия листа и энтропия черной дыры? |
| В 1972 году физик Джейкоб Бекенштейн разработал изящную формулу для расчета энтропии черной дыры. Формулировка энтропии известна как энтропия Бекенштейна-Хокинга и пропорциональна площади горизонта событий черной дыры. Это один из немногих ярких примеров связи геометрии с энтропией. Позже, в 2008 году, структура формулы энтропии Бекенштейна-Хокинга была сформулирована ученым Георгом Дж. Шмитцем с использованием геометрических соображений геометрической сферы, основанных на непрерывном трехмерном расширении функции Хевисайда, которая опирается на концепцию диффузного фазового поля. интерфейсы. Мы следовали междисциплинарным подходам для количественной оценки сложности листьев. Мы вывели сложность листьев растений как геометрическую энтропию с информационной точки зрения, приняв идею формулировки Бекенштейна-Хокинга энтропии черной дыры Георга Дж. Шмитца. Наши результаты опубликованы в журнале PLOS ONE. |
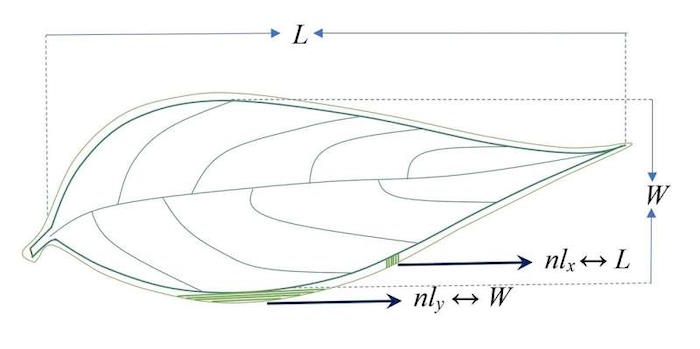
| В то время как воспринимаемая геометрия на четком интерфейсе объекта (макро) создает евклидову иллюзию реальной формы, понятие диффузных интерфейсов (микро) позволяет понять реалистичную форму объектов. Мы воспринимали границу листа как узкую диффузную границу раздела лист-среда, которую мы считаем аналогичной диффузной границе раздела в теории фазового поля. Используя концепцию мереотопологии, менее известной дисциплины в научном мире, которая связывает статические отношения между объектами логическими выражениями, истинными или ложными, мы в конечном итоге получили геометрическую энтропию для геометрического круга, которая затем преобразуется для геометрического круга. энтропия листьев растений. Наш подход был чисто теоретическим и основан на непрерывном двумерном расширении функции Хевисайда и функций фазового поля на узкой диффузной границе листовой среды. Описание формы диффузной границы раздела лист-среда достигалось путем статистического распределения градиентов в диффузной границе раздела. Выражение геометрической энтропии пропорционально периметру листа и квадратному корню из площади листа и соответствует известному показателю рассеченности листа. |
| Каковы потенциальные применения геометрической энтропии? |
| Геометрическая энтропия — это неотъемлемая мера сложности, которая превосходит другие сложные геометрические морфометрики. Он не требует трудоемких методов предварительной обработки и предлагает перспективный метод количественной оценки степени изменения формы листьев, таких как глубокая лопасть, рассеченность, зубцы и периметр листа. Обычные геометрические морфометрические методы в основном сосредоточены на гомологичных признаках, которые чувствительны к размеру листа, а не к форме листа, что ограничивает их надежную применимость в различении форм листьев на таксономических уровнях. Однако, несмотря на небольшие недостатки, геометрическая энтропия представляет собой потенциальный метод классификации форм листьев на уровне рода. |
| Мы надеемся, что это может стимулировать биологов растений к изучению его потенциального использования в таксономии. Морфология листьев является наследуемым признаком растений и влияет на поглощение света, транспорт сока и фотосинтез. Растения оптимизируют структуру листьев, чтобы повысить эффективность обмена энергии и максимизировать ассимиляцию углерода, размножение и устойчивость. Мы знаем, что знание сложных форм листьев имеет огромный потенциал для понимания геометрии и ее связи с захватом энергии. Поскольку сложные листья обладают большей адаптивной стабильностью в изменяющейся среде, мы предлагаем нашу геометрическую энтропию в качестве производного признака растения для описания сложности листьев и адаптивной стабильности. Это поможет в исследованиях по дизайну искусственных листьев для генетический инженерии оптимальных форм листьев в будущем. |
| Источник |






